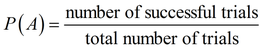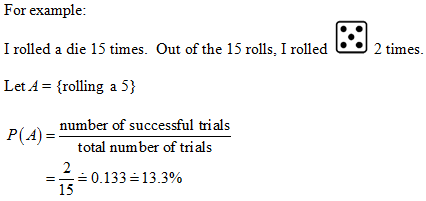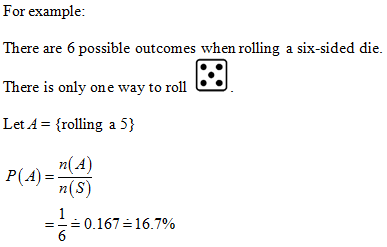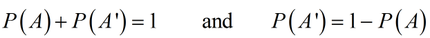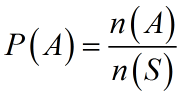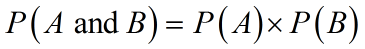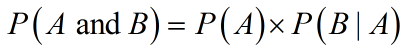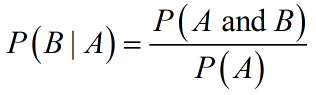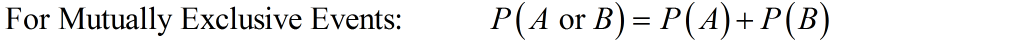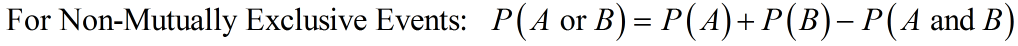MDM4U Unit 3:
Probability
3-1 Basic Probability Concepts
Learning Goal:
I can ...
- explain and apply basic probability concepts to real-world applications
Lesson:
Read and take notes as necessary:
1) Basic Understanding of Terminology
Probability is the branch of mathematics that attempts to predict what might happen.
A probability experiment is a process consisting of a number of trials in which clearly distinguishable outcomes (possible results) are observed. Outcomes are usually equally likely to occur.
The sample space, S, of an experiment is the set of all possible outcomes.
An event is the set of outcomes for which you want to know the probability. Events are usually written with capital letters.
The probability of an event is a measure of the likelihood that the event will occur.
Probabilities can be written as fractions, decimals, or percents.
There are 3 types of probability:
1) Basic Understanding of Terminology
Probability is the branch of mathematics that attempts to predict what might happen.
A probability experiment is a process consisting of a number of trials in which clearly distinguishable outcomes (possible results) are observed. Outcomes are usually equally likely to occur.
- For example, you could perform a probability experiment in which you are rolling a six-sided die. If you roll the die 10 times, that means you performed 10 trials. The possible outcomes are 1, 2, 3, 4, 5, or 6. The outcomes all have an equal likelihood of happening.
The sample space, S, of an experiment is the set of all possible outcomes.
- For example, you could perform a probability experiment in which you roll 2 six-sided dice. You could roll a 1 on the first die, and a 1 on the second die (1, 1); you could roll a 4 on the first die and a 3 on the second die (4, 3); etc. The sample space would be:
- (1, 1) or (1, 2) or (1, 3) or (1, 4) or (1, 5) or (1, 6) or
- (2, 1) or (2, 2) or (2, 3) or (2, 4) or (2, 5) or (2, 6) or
- (3, 1) or (3, 2) or (3, 3) or (3, 4) or (3, 5) or (3, 6) or
- (4, 1) or (4, 2) or (4, 3) or (4, 4) or (4, 5) or (4, 6) or
- (5, 1) or (5, 2) or (5, 3) or (5, 4) or (5, 5) or (5, 6) or
- (6, 1) or (6, 2) or (6, 3) or (6, 4) or (6, 5) or (6, 6)
- There would be 36 possible outcomes in the sample space.
An event is the set of outcomes for which you want to know the probability. Events are usually written with capital letters.
- For example, when you roll 2 six-sided dice, let's say you want to know the probability of rolling a sum of 3.
- Let A = a sum of 3
- A = { (1, 2), (2, 1) }
- That means that event A will occur if:
- the first die is a 1 and the second die is a 2; or
- the first die is a 2 and the second die is a 1
The probability of an event is a measure of the likelihood that the event will occur.
- If P(A) = 0, that means it is impossible for event A to happen.
- If P(A) = 1, that means it is certain that event A will happen.
- Most events in probability studies fall somewhere between 0 and 1.
- Probabilities can never be less than 0 or greater than 1.
Probabilities can be written as fractions, decimals, or percents.
- For example, a 70% chance of rain tomorrow means the same as a probability of 0.7 or 7/10.
There are 3 types of probability:
- Experimental Probability is determined using the results of a probability experiment.
- Theoretical Probability is determined using an analysis of all possible outcomes.
- Subjective Probability is an estimate of an event's likelihood based on intuition and experience.
Our focus will be on Theoretical Probability in this course.
A useful and important concept in probability is the complement of an event. The complement of event A is called A'.
- If A = {rain}, then A' = {no rain}
- If B = {rolling a 6}, then B' = {not rolling a 6}
2) Probability Examples
Practice:
1) Complete the following textbook questions:
- Page 312, # 1, 2, 4, 5, 6, 7, 11
3-2 Probability Using Counting Techniques
Learning Goal:
I can ...
- extend my understanding of basic probability to use the counting techniques discussed in Unit 2
Lesson:
Read and take notes as necessary:
1) Review
Remember the basic probability formula:
1) Review
Remember the basic probability formula:
where
To determine n(A) and n(S), you may use any of the counting techniques discussed in Unit 2:
2) Examples of Probability Using Counting Techniques
In the previous lesson, some basic probability questions were covered. However, some probability questions can get more complicated.
- n(A) is the number of ways that event A can happen, and
- n(S) is the total number of possible outcomes.
To determine n(A) and n(S), you may use any of the counting techniques discussed in Unit 2:
- Factorials
- Permutations
- Combinations
- Tree Diagrams
2) Examples of Probability Using Counting Techniques
In the previous lesson, some basic probability questions were covered. However, some probability questions can get more complicated.
Work:
3-3 Dependent and Independent Events
Learning Goal:
I can ...
- determine the difference between dependent and independent events; and
- apply the appropriate strategy
Lesson:
Read and take notes as necessary:
1) Understanding the Terminology
Compound Events are events that involve two or more separate events. Examples of probability questions that involve compound events are:
Compound events can involve events that are independent, or events that are dependent.
Independent Events: The occurrence of the first event has no effect on the occurrence of the second event.
1) Understanding the Terminology
Compound Events are events that involve two or more separate events. Examples of probability questions that involve compound events are:
- If you have two exams next Tuesday, what is the probability that you will pass both of them?
- If you flip a coin repeatedly and get heads 99 times in a row, what is the probability that the next toss will be tails?
Compound events can involve events that are independent, or events that are dependent.
Independent Events: The occurrence of the first event has no effect on the occurrence of the second event.
- The compound probability of two independent events can be calculated using the product rule for independent events:
Dependent Events: The occurrence of the second event depends on the outcome of the first event.
- The conditional probability of event B is the probability that B occurs, given that A has already occurred.
- P(B|A) means the probability of B, given that A has already occurred.
this can be rearranged to solve for the probability of B, given that A has already occurred:
2) Examples of Independent and Dependent Events
The first example is for Independent Events:
The first example is for Independent Events:
Practice:
3-4 Mutually Exclusive Events
Learning Goal:
I can ...
- identify when events are mutually exclusive, and
- apply the appropriate strategy to solve real-world problems
Lesson:
Read and take notes as necessary:
1) Understanding the Terminology
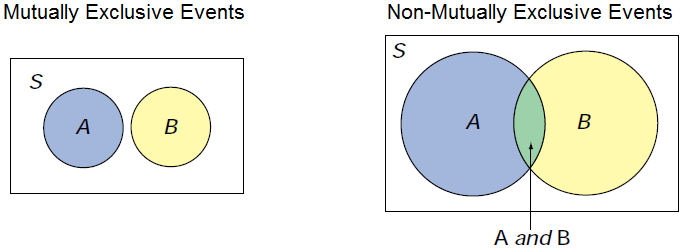
Events are mutually exclusive if they cannot occur at the same time (the sets are disjoint). For example:
For mutually exclusive events, you can calculate the probability of either event A or event B occurring using this formula:
1) Understanding the Terminology
Events are mutually exclusive if they cannot occur at the same time (the sets are disjoint). For example:
- In a race, event A is coming in first place, and event B is coming in third place.
- Both event A and event B cannot occur at the same time.
- Therefore events A and B are mutually exclusive.
For mutually exclusive events, you can calculate the probability of either event A or event B occurring using this formula:
Events are non-mutually exclusive if they can occur at the same time (the sets have an intersection). For example:
- When you roll 2 dice, event A is rolling an 8, and event B is rolling doubles.
- Both event A and event B can occur at the same time (when you roll two 4s).
- Therefore events A and B are non-mutually exclusive.
For non-mutually exclusive events, you can calculate the probability of either event A or event B occurring using this formula:
2) Examples of Mutually Exclusive Events
Practice:
1) Complete the following textbook questions:
- Page 340, #1 - 3, 5 - 8, 13, 14
Unit 3 Review
If you need extra review practice, feel free to pick and choose from any of these questions: